The Development of the Thesis

EPC: Emergent Personalized Content in Video Games

Simone Guggiari - September 11th, 2019

This is a devlog of the development and the results of my Master Thesis, entitled Emergent Personalized Content in Video Games, that I worked on at the Game Technology Center between October 2018 and April 2019.

If you like what you find here and are interested in a more in-depth treatment of the topic, you can see my Master Thesis here, and the final presentation here (which somewhat maps with this article). You can also play the prototype developed as part of this project here.

A big thank you to my supervisors: Prof Dr. Robert W. Sumner, Dr. Fabio Zünd, Henry Raymond. 

A screenshot from the final game.

The Origin

It all started at Gamescom 2018 (Cologne, Germany) when I was exposing another project my team and I were showcasing (That Failed Bank Robbery). I would sometimes wander off to find new exciting games to try out. I went to the Indie Arena Booth and found a game that immediately stood out: Bad North. I loved the aesthetics and the gameplay, but most of all, I was utterly fascinated by the islands. The developer, Oskar Stalberg, told me that they were procedurally generated.

Oskar Stalberg's procedural island generation, the inspiration for this thesis. Image from his twitter (@OskSta).
The islands as seen in the game Bad North. Do check it out, it's one of the best games I ever played.

Upon doing some more research, I found a talk where he explained the algorithm he used, which was the Wave Function Collapse (WFC), developed by Maxim Gumin in 2016.

The algorithm, in its original form, takes a small patch of an image as input denoting a pattern and can generate output images with local similarity to the input. The iterative visualization is especially mesmerizing. Just check out its beauty:

An iterative visualization of the WFC algorithm. The pixels are in a "superposition" (blended colors) at the beginning and are iteratively collapsed to a single color. The constraints are then propagated. Image form Maxim's Github page.
More examples of the output produced by the WFC algorithm.

WFC is a probabilistic algorithm that creates either images or complex structures made out of tiles by collapsing into slots one out of many possible modules. Once a module is placed, depending on the boundary, constraints are propagated to neighboring cells, possibly causing more collapses. You can find a detailed explanation of the algorithm on Maxim’s Github page and several examples on his twitter.

I felt as if I had discovered a goldmine, and knew right then and there I wanted to do my master thesis around this topic. I had always been fascinated by procedural generation and the different algorithms that allow you to generate content dynamically. Several of my previous games featured procedural generation of some sort (even my first game, Splat it!). I had, however, never come across to an algorithm this beautiful and powerful.

Although constraint propagation is deterministic, when one slot has multiple possible modules that could fit there, the algorithm has to choose one among them. There are several ways to select which module to place. I thought that by assigning weights to each module and then tweaking those weights dynamically depending on the player. Doing so, one could use the algorithm to generate different types of content for each player.

If we could learn a mapping between the player in-game behavior (and therefore his/her underlying preferences) and some set of weights to use in the procedural algorithm, we could generate levels that adapt to the user. Such levels would provide a more engaging experience.

I decided I would create an algorithm to adapt those weights dynamically . I would also develop a game prototype that would help us test out the effectiveness of this method by performing different user studies. The ideas were formalized in the thesis proposal, and the project started.

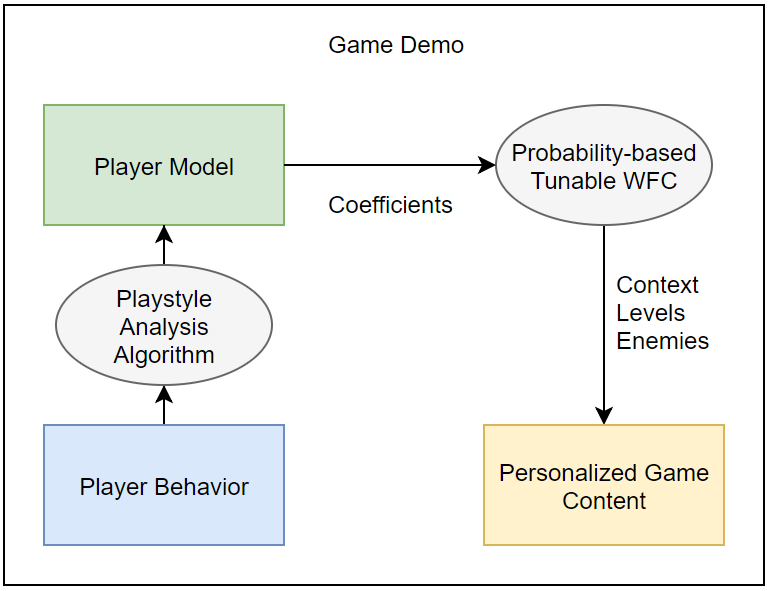
The initial flowchart explaining the different components of the algorithm and how data moves from one stage to the next.

This flowchart explains the basic idea: when players engage in a game, they exhibit some behavior. One could analyze such behavior to build a model of the player, to be able to categorize them. By using the coefficients in this model, one could tune different procedural content generation algorithms, that – if configured correctly – would then generate personalized game content.

One of the other reasons for starting this project (other that I wanted to get my master) was one observation. Mainstream services, such as Amazon, YouTube, Netflix, have an incredible amount of data about our preferences. They use such personal preferences and the crowd’s wisdom to create recommender systems that provide individual users with different and personalized content. Leaving aside some of the more shady uses of such information, one could apply similar methods to videogames, which, by their nature, are such an interactive medium. One could then improve the experience for the player beyond just recommending which game to play next, by considering these preferences.

Overview

This is a brief overview of the topics I’ll talk about in this post:

I’m going to start by quickly touching upon games that use similar techniques to adapt the game to the user.

I’m then going to describe the pipeline and the different stages of our method, and then delve more into the player encoding, the content generation, and its adaptation.

Afterward, I’m going to show the prototype framework developed to test out the mechanics. I’m also going to show the final more polished game created to use as a training ground and to collect user data.

To conclude, I’m going to show the data collected in the study, and talk about the results and some insights. A look at what might come in the future concludes this article.

Other Adaptive Games

Some games already pioneered game systems that adapt to how the players behave.

One example of this is, most notably, the game “Left 4 Dead” developed by Valve. It features an AI system called “The Director”. This system creates a simple 1D coefficient for every player (the stress level) and then modulates the frequency and amount of enemy spawned based on this coefficient. The goal is to generate peaks (or how the developers call them, “action spikes”) of intensity and moments of relaxation. This helps provide optimal pacing for the game and draw players in. You can read more about this system in the presentation The AI Systems of Left 4 Dead.

An image from the game Left 4 Dead.
One-dimensional stress coefficients for each player in the game and the four phases used to modulate the gameplay.
The population of enemies over time, as modulated by the game system, with relax phases marked.

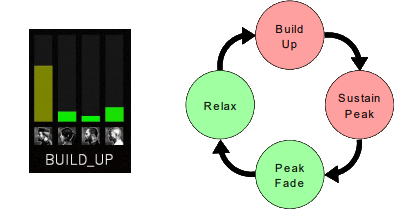
Several other games also adapt to the users, but this is often limited to difficulty tuning rather than content. This is understandable, as creating content is an expensive and time-consuming process. Creating more content that might not be seen by the user is not very cost-effective for a studio. Procedural generation algorithms solve this problem, as once the generation algorithm is in place, new content can be generated almost for free.

Personalization Algorithm Overview

We now show a high-level overview of the different stages of the personalization algorithm. One of the goals of the thesis was not to create a system specific to only one game or a game genre but to develop a method general enough to be applied to a wide variety of games. Any result obtained with an algorithm too specific to a single game couldn’t be generalized and results couldn’t be extrapolated.

Although some aspects have to be tuned to the particular game in this thesis, the pipeline is general enough to be applied to almost any game.

The primary pipeline is the following:

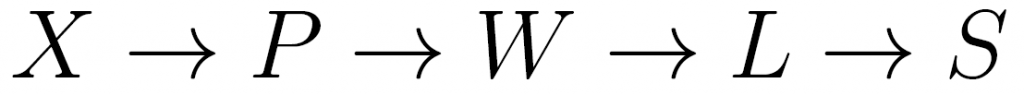
The 5 stages of the pipeline, from recorded metrics to player encoding, level generation, and finally user satisfaction.

We define five multi-dimensional spaces, whose coefficient describe a particular aspect along the pipeline. In each space, we represent a set of coefficients as a single point. One then can move from one multi-dimensional space to the next by using a mapping function that transforms a point from one space to the next.

Since we have 5 spaces, we need 4 functions.

The spaces are explained below:

  • X: Recorded metrics
    This point represents the set of game-metrics recorded per player i on a particular level or play-session j.
  • P: Player encoding
    The coefficients used to describe the personality and preferences of a player i.
  • W: Generation coefficients
    The coefficients used in the procedural level generation to tune the algorithm.
  • L: Level
    The result of the generation, namely a piece of content (in our case: a level) encoded by coefficients.
  • S: Satisfaction scale
    A scalar representing the level of satisfaction or enjoyment experienced by a player upon playing the particular generated level.

The 4 functions that map between spaces are the following:

  • C: (X -> P): Player model function
    Maps the metrics recorded about a player to a player model.
  • F: (P -> W): Adaptation function
    Generates the coefficients to use in the procedural generation algorithm based on the values of the player model.
  • G: (W -> L): Generative algorithm
    The procedural algorithm that takes the coefficients in the previous stage and generates the content to be experienced by the user. In this particular thesis, we use the WFC algorithm to create the levels, but one could swap this algorithm with another one to produce other types of content.
  • R: (L -> S): Rating function
    This is a fancy name to say “player”. The player plays the level and, upon completion, gives a score (a rating) to the content he was presented with to help the algorithm tune and generate more appealing content.

Player Models

We did a lot of research into possible ways to encode players as a set of coefficients and looked at several models that categorize players along axes or among a set of possibilities.
Some of the models we looked at were meant explicitly for players, whereas some were more applicable general models of personality.
Some of the models analyzed include:

Raph Koster discusses several of these models in his excellent book A Theory of Fun when he describes why we play games and tries to distill the essence of fun.

There also is an extremely handy article by Bart Stewart on most of the models mentioned above and how they relate to each other. This article was a great inspiration for this thesis, as he distills what he calls a “Unified Model of Personality and Play Style”.

In the end, we decided to base our model on the 4 Bartle Types to avoid unnecessary complexity, and because the model was widely accepted.

This model splits players along two axes:

  • on one axis, players are divided about the modality with which they interface themselves with the game: if they prefer more to act ON the game, or if they prefer interacting WITH it
  • on the other axis, the players are split according to the type of content they prefer: are they more interested in dynamic players, or on the static game world?

By diving the cartesian space along those axes, one obtains 4 quadrants, and to each Bartle gives a distinctive name:

  • Killers enjoy acting on players
  • Achievers prefer acting on the world
  • Explorers like interacting with the world
  • Socializers are interested in interacting with the players

One can try to approximately split typical game mechanics by quadrant, although, of course, this is only a very coarse generalization. It nonetheless helps better understand what types of players might engage with our game and therefore better design it.

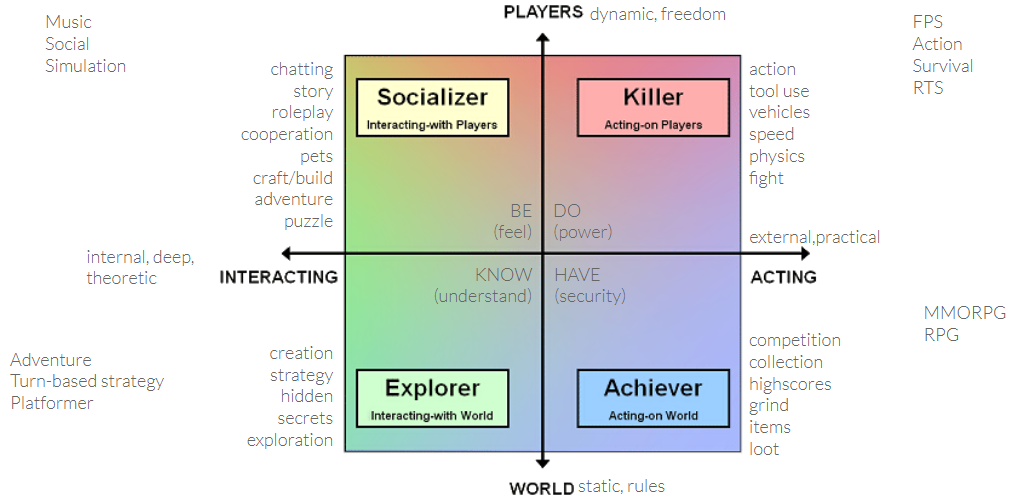
The 4 quadrants described by Richard Bartle, annotated with the inner need, typical game mechanics, and game genres.

One aspect I was particularly fascinated with is how each of the 4 player types described by the above model closely maps with a specific need:

  • Killers want to feel powerful (DO), and do so by imposing themselves upon others in the game world
  • Achievers want to feel safe (HAVE) and achieve this by collecting status-tokens and other game items.
  • Explorers want to understand the dynamics of the game (KNOW), and generally seek knowledge.
  • Socializers want to feel part of a community of other players (BE).

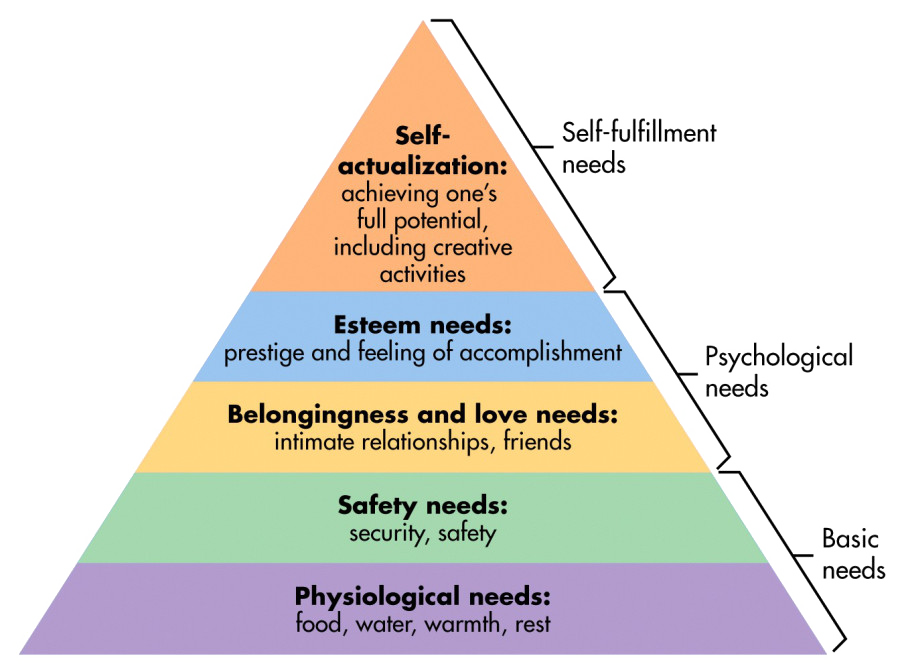
Quite surprisingly, those needs closely map to Maslow’s Hierarchy of Needs, that, after physiological needs such as food and water, includes:

  • Safety (security): similar to what the Achiever wants.
  • Belongingness (relationship, friends): similar to the Socializer type.
  • Esteem needs (prestige, a feeling of accomplishment): similar to Explorer type.
  • Self-actualization (achieving full potential, doing): similar to Killer type.
Maslow's Hierarchy of Needs. Image from simplypsychology.org
I want to specify that putting “Killer” at the top of the pyramid feels very weird indeed. However, although the name is not very suited, if you understand what Bartle calls “Killers” as individuals that want to act, one can start to see a resemblance.
 
With this, an interesting idea starts to form: we can see games as a form of need satisfaction. Games, in this view, are used by players to fulfill the needs of things they covet.

Our Model

Our model is based upon Bartle’s Taxonomy but differs in specific ways. We don’t restrict traits to be on a single axis, meaning that one player can be both interested in players and the game world, with different priorities.

We represent the metrics recorded in our game as a 4-dimensional vector x=(K,A,E,S), where the 4 numbers are mapped to how often a given player acted in each of the categories mentioned above.

  • K is the number of actions exhibiting aggressive/killer-like behavior (fighting, shooting, killing)
  • A is the number of actions exhibiting achiever behavior (collecting, looting, crafting)
  • E is the amount of explorer-like behavior (exploring, looking for secrets, solving puzzles)
  • S is how much social behavior is shown (in our game, this metric is ignored as there is no multiplayer aspect)
A visual representation of our player model. Although we have 4 coefficients, we normalize them, effectively reducing to only 3 degrees of freedom. By constraining each coefficient in the range [0,1], our model becomes a tetrahedron. Each player is then a point inside this tetrahedron. His coefficients represent his/her barycentric coordinates.

We can then generate the player model by simply normalizing each coefficient individually, based on how other players behaved.

If we assume that a game, by design, forces each player to take a certain number of actions, we notice that there is an underlying bias in the recorded numbers. An example of this is that by spawning aggressive enemies, the player is forced to kill them. We are therefore not interested in the absolute number of actions per category, but rather in the deviation each player exhibits with respect to the population of players. This measure expresses how much a player tries to do a particular action “more” or “less” than the game forces the player to do when played neutrally, without any preference.

We assume a normal distribution for each parameter and calculate the coefficient p_i as a normalized factor of deviation with the formula shown below.

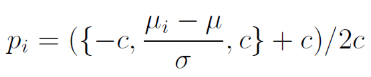
The simple formula used to normalize each metric recorded to form the player model. It is a measure of how many standard deviations a particular player with value \mu deviates from the underlying population. The range [-c, c] is mapped to [0, 1]. C is usually 3.3
Visual representation of a normal distribution. Note how the majority of values falls within 3 standard deviations from the mean.

Content Generation

We had a few constraints when looking for a suitable content generator. The algorithm had to be:

  • procedural since this provides an infinite amount of content and each piece of content is cheap
  • general enough to be able to generate multiple types of content (not only levels)
  • produce varied output
  • be controllable (as we needed to tune it)
  • fast, since we’re using it in a real-time application

The perfect candidate was the Wave Function Collapse, mentioned previously. You can read about WFC on Maxim Gumin’s Github page. The basic idea is to generate images given a sample bitmap as input that specifies constraints, such as which pixels can appear close to each other and which cannot. It’s a sudoku-solver for pixels or modules.

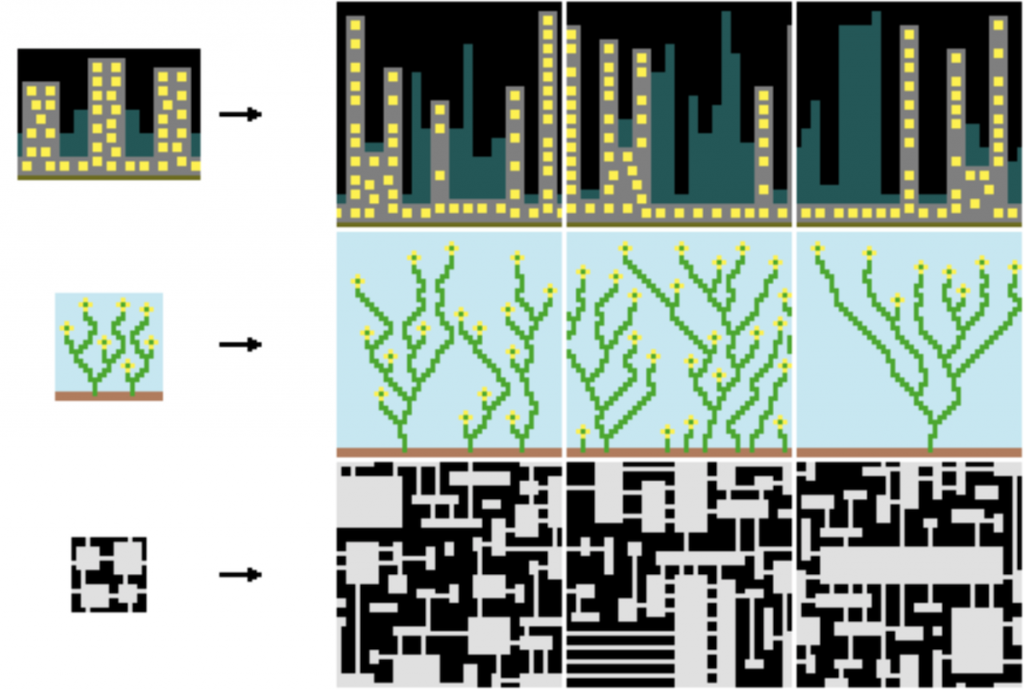
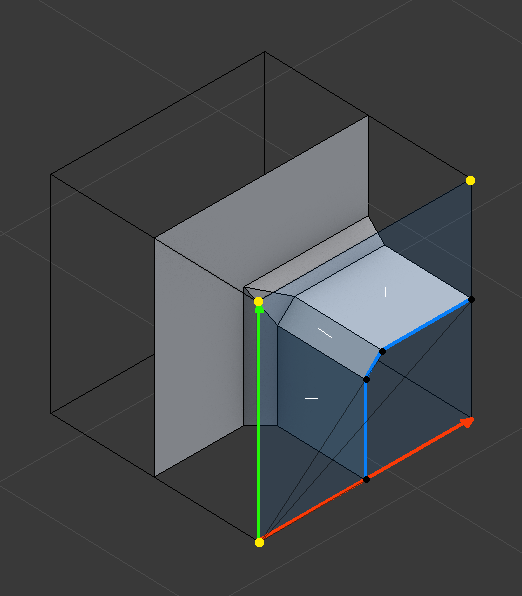
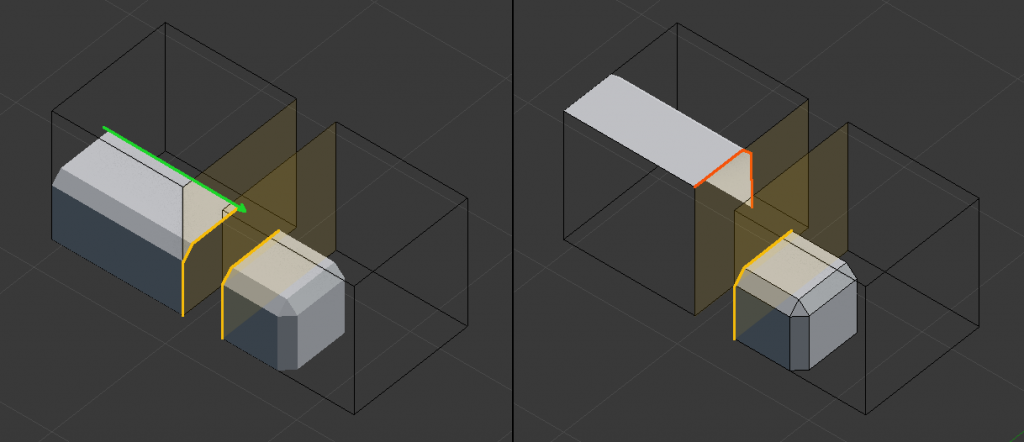
Several ports were already made to port the algorithm to 3D. They either use voxels (the pixel concept adapted to 3D) or a more sophisticated method of modules embedded into voxels that could then be combined.
You can see some of the results of these methods below:

Above: Escher-esque buildings generated by Maxim Gumin. Below: Bad North's islands, and Caves of Qud (right).

There are many advantages to using the WFC algorithm. Since many games use modular models to create levels and reuse content, any tileable level can be generated with this algorithm by expressing the right constraints. This means that this algorithm could be used to create a massive variety of levels used in games, which is quite impressive.

In the following flowchart, you can see the different generation steps in our method:

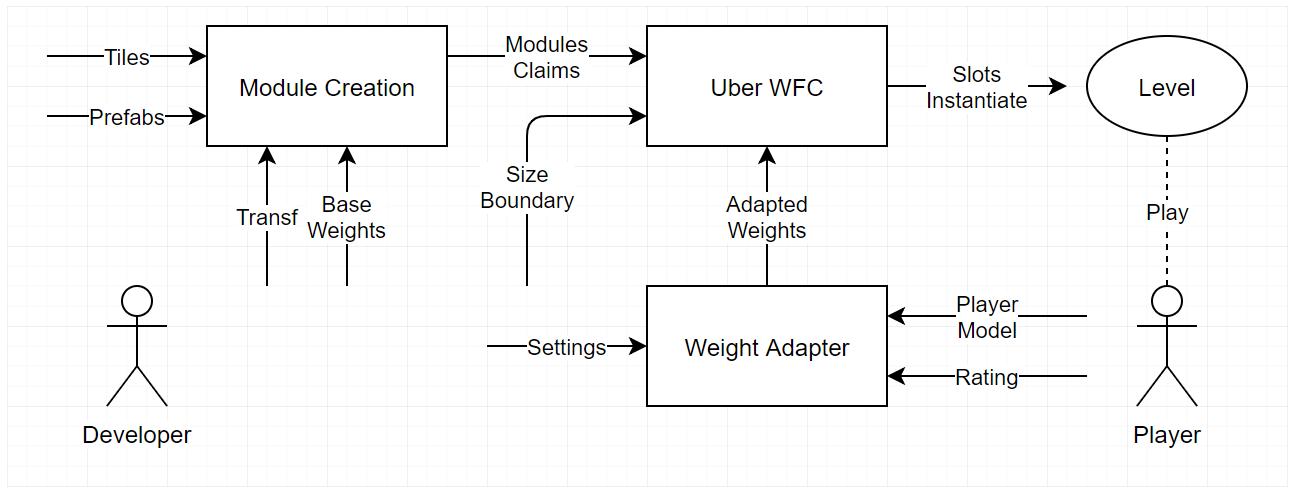
A high-level overview of the generation process in our system. The developer and the players interact with 3 main components: the module creation (static), the WFC (dynamic), and the weight adapter (that works with the player models).

We start by providing tiles and prefabs to the Creation Module, as well as transforms and base weights for each tile. The Creation Module uses this information to augment each tile with all the possible rotation configurations, as well as generate adjacency constraints. The base weights are used as manual input to tweak the base probabilities of placing each module.

The generated modules are then forwarded to the WFC algorithm, which together with the weights, generates a suitable instantiation of a module per slot. This configuration can be instantiated as a level and given to the player to play.

Upon finishing a level, the player can rate the level just completed. The rating is fed into the Weight Adapter Module, that modifies the player model given the new data and changes the weights based on the rating and the behavior of the player.

The adapted weights are then re-fed into the WFC generation algorithm to instantiate the next piece of content for the user to play.

A 3D hashing method used by the Module Creation component to find modules that can fit together. The interested reader can read about the specific approach and implementation in the master thesis.
A visual representation of problems that arise by naively assigning a hash index to each side. Rotations change suitability of adjacent modules.

TileSet

One significant aspect of this thesis was to develop a tileset suited to generate playable levels, that were varied enough to provide different challenges and gameplay to each user. There were several iterations of the tilesets, as well as several tests to classify the suitability of a given tileset. We don’t go over them here and present only the results instead. The interested reader can find the details in the Master Thesis.

Several iterations of tilesets to be used in the game. Playability was a big concern.
The final set of tiles used in the game. There are a total of 14 different types. Each type features 4 variations to provide visual difference and different obstacle placement. The algorithm chooses among the available prefabs for each tile.
A generated level. Left: the underlying assembly of simple tiles (shown previously) as seen by the algorithm. Right: the detailed prefabs instantiated for the player to see.
Different levels generated procedurally by the algorithm by changing the weights of the individual modules. Some examples have extreme weights to show the range of possible variation.

You can see from the previous images that extremely different types of levels can be generated. Although a very reduced type of tileset is used (only 14 different types), by changing the weights of the instantiation, one can dramatically impact the map layout, the obstacles, and the pathways. This then alters how the game plays.

Adaptation

The goal of the adaptation stage is to find optimal parameters w* that once fed into the procedural algorithm, will generate the level producing the maximum enjoyment for the player.

We can express this problem as a maximization search over a space in which the target function is only known at specific discrete points.

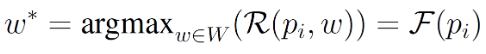
There are several ways to go about this, and we decided on a simple approach of looking at what similar players liked.

We produce a weighted average of what players with similar models enjoyed, scale it by the rating and divide it by the distance. Higher-rated levels should have more impact, and so should more similar players. We only consider points within a certain distance to ignore players with a completely different playstyle.

This assumes that players exhibiting similar behavior will enjoy similar levels and that the rating function is linear. These assumptions might be incorrect in some instances, but for our case, they are a reasonable approximation.

We can then generate a new point by straightforward gradient ascent, taking a step in the direction in which we believe the enjoyment is more likely to increase. The step-size is inversely-proportional to the rating: if the user is satisfied, we try to generate a new point close to the level already played. If the user is not, we try to move away from levels with this particular configuration as quickly as possible.

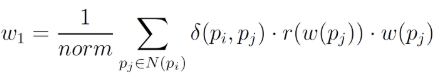
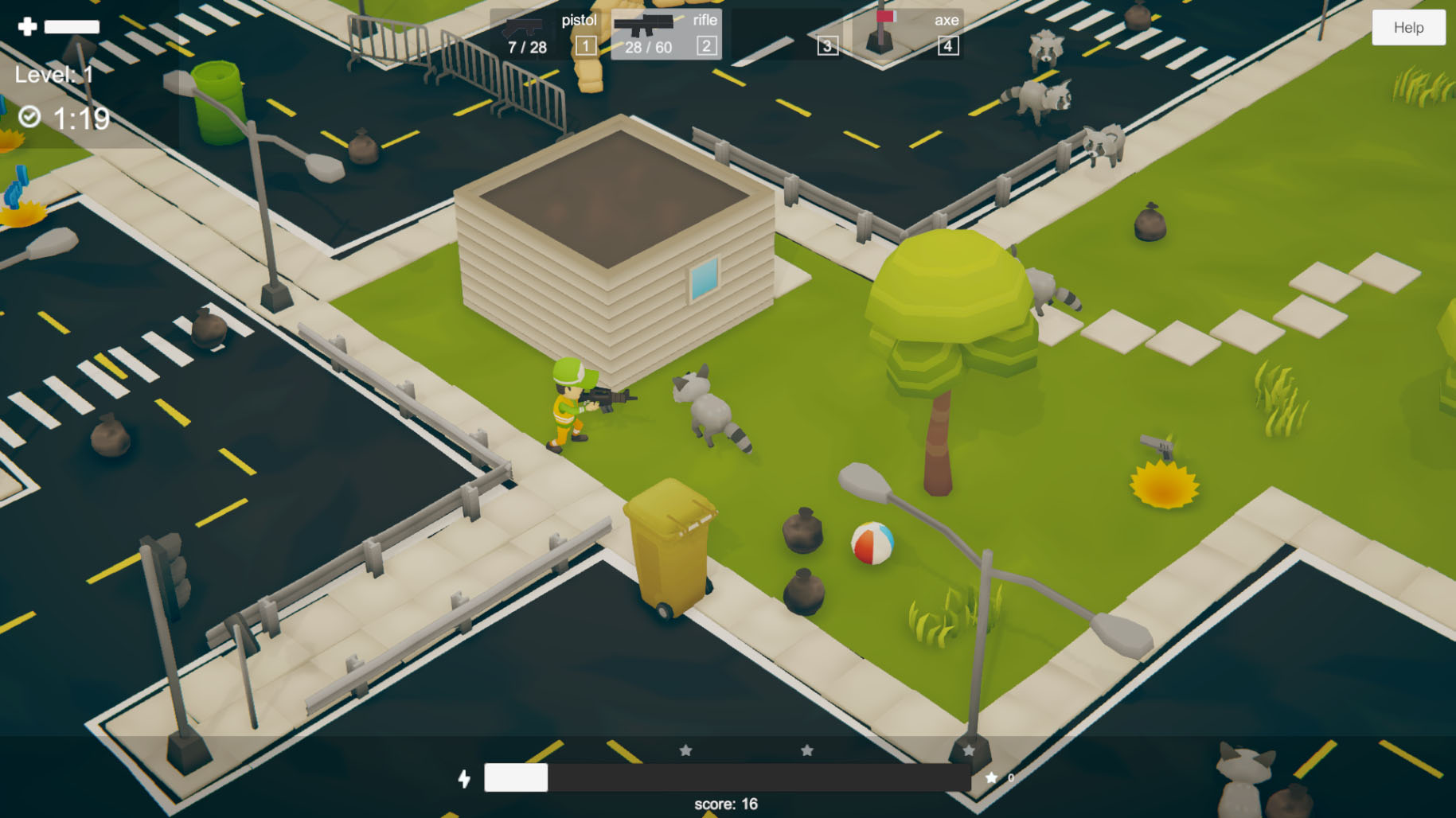
The Game

The game started as a very general framework with a top-down perspective, in which the player could do most of the actions found in this sort of game, including

  • Movement (walk, run, sneak, vault, jump)
  • Equipment use (guns, melee weapons, grenades)
  • Basic Enemy AI (patrol, chase, attack)
One of the early iterations of the game framework, with weapons, resources, crafting, turrets, and usable items.

Once the design settled, the game was polished and stripped down to a more focused experience, to appeal to a broader audience during our play-tests.

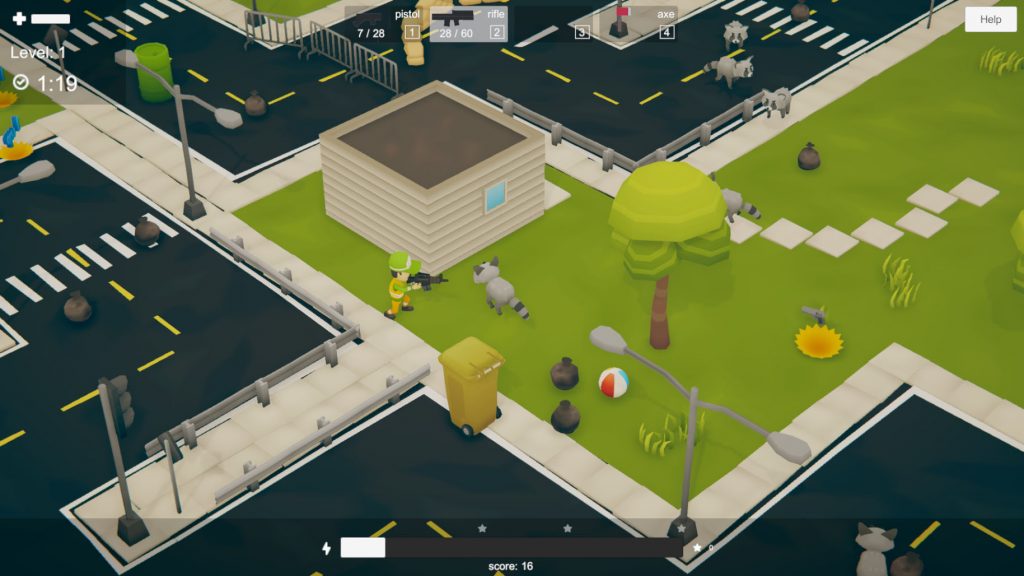
In brief, the final game is a top-down shooter in which the main character must run, explore, collect items, and fight enemies to earn enough points before time runs out.

You play as Gianni, a garbage collector that is trying to restore the City of Cleanolandia to its former glory, by defeating the angry raccoons that have littered everywhere. You can collect trash, find powerups, weapons and special items, and fight said raccoons.

The raccoons aren’t aggressive by default since we don’t want to force the player to fight.
The player obtains points by performing different types of actions and can beat levels with several strategies. For instance, he can win without fighting or collecting anything but only exploring.

You can see a few screenshots and gameplay videos below.

A screenshot from the final game.
All the props used in the game.
If you have read some of my other posts, you now I like to use a single texture for every asset in the whole game. Here it is!
Concept art made during the ideation process of the game by Wenart Gunadi.

Results

We run several user studies at different points during the thesis to obtain early feedback and steer the thesis in the right direction. The thesis lasted 6 months, and we performed user studies on months 3, 4, and 5. The results are treated in depth in the thesis. Here, we only quickly glance over some interesting insights.

The main research question was “Does our personalization algorithm increase the enjoyment of the experience?“

First Study

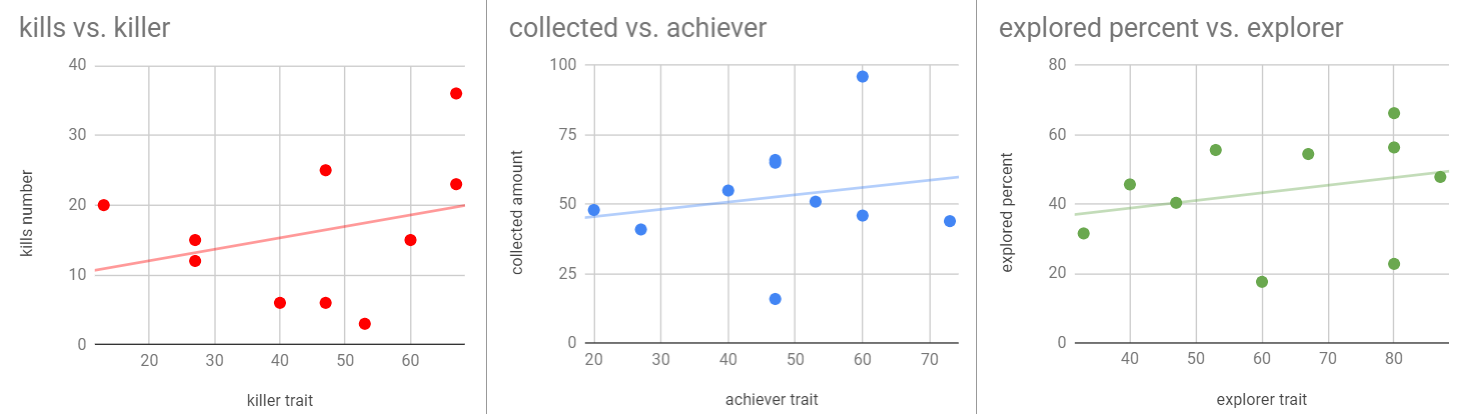
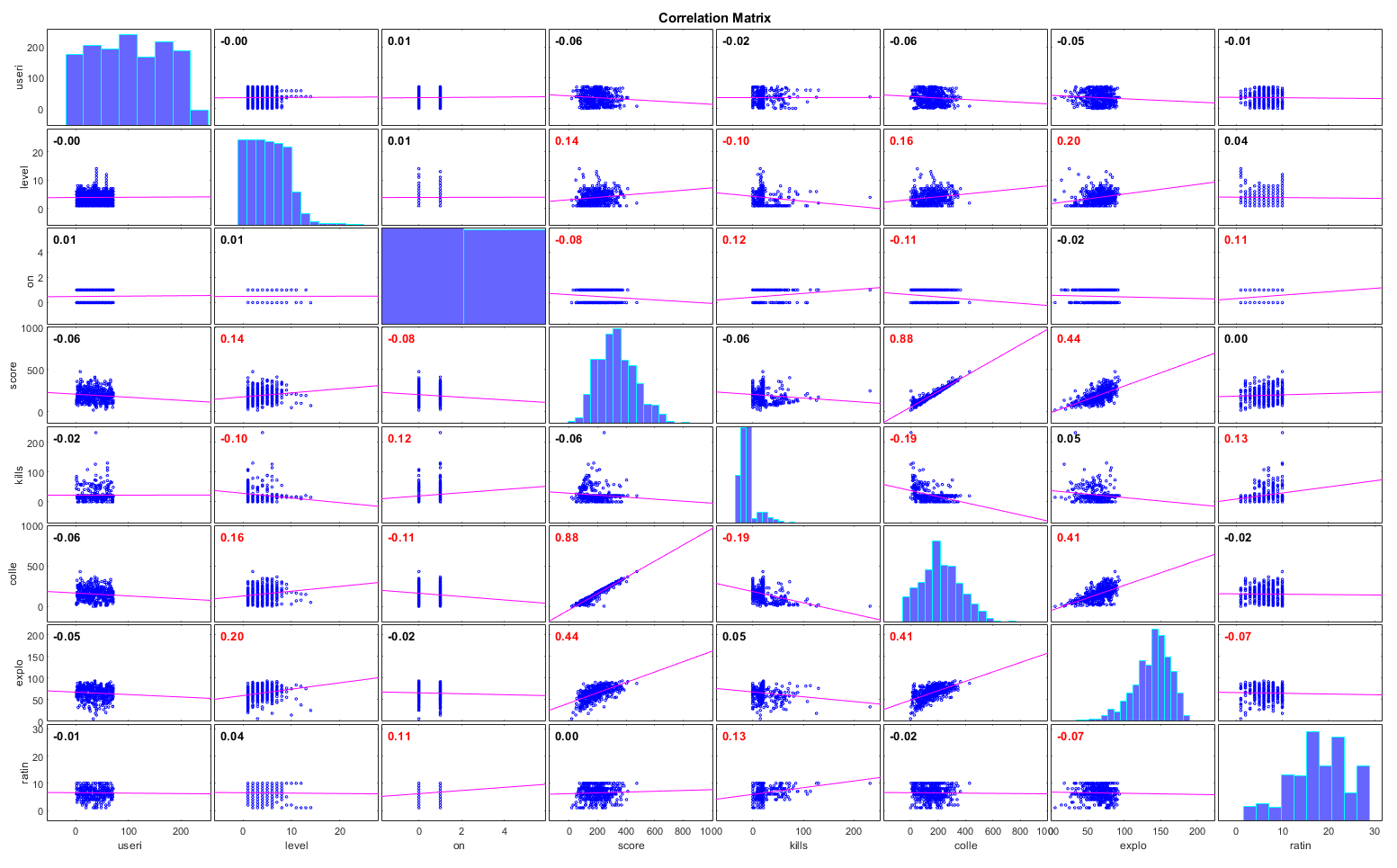
In the first user study, we focused on collecting data about the different player types. This was done to see if there was a correlation between the score obtained in the questionnaire categorizing players into one of the four Bartle Types, and the actions taken in-game. As you can see from the graphs below, other than having a small number of users and data-points, there was a very weak correlation between the two. This helped us steer the development of the game and algorithm not to rely too much on the player self-evaluation, and to make the game more appealing to obtain a larger data-set.

Early results showcasing the correlation between the reported score in each category and the number of in-game actions for a given type.

Final Study

In the final study, we had 96 participants play over 570 rounds of the game. We had users fill out a personality questionnaire as well as play several rounds of the game. We then pruned the early rounds since players were likely to be learning the game mechanics in this period and analyzed the remaining data.

You can see the questionnaire results below:

The dominant category for our population sample.
More than half of our players play regularly. One quarter rarely or never play.
The detailed distribution of scores of membership to each category.

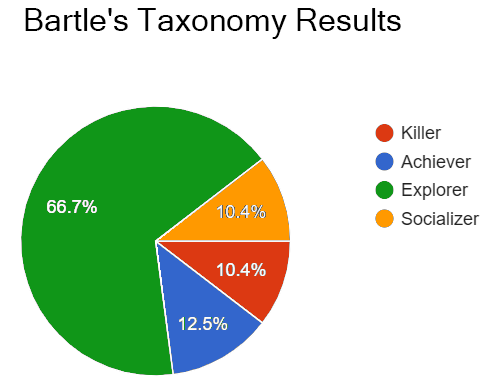
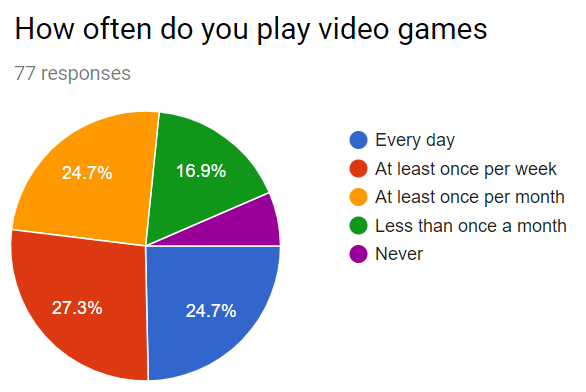
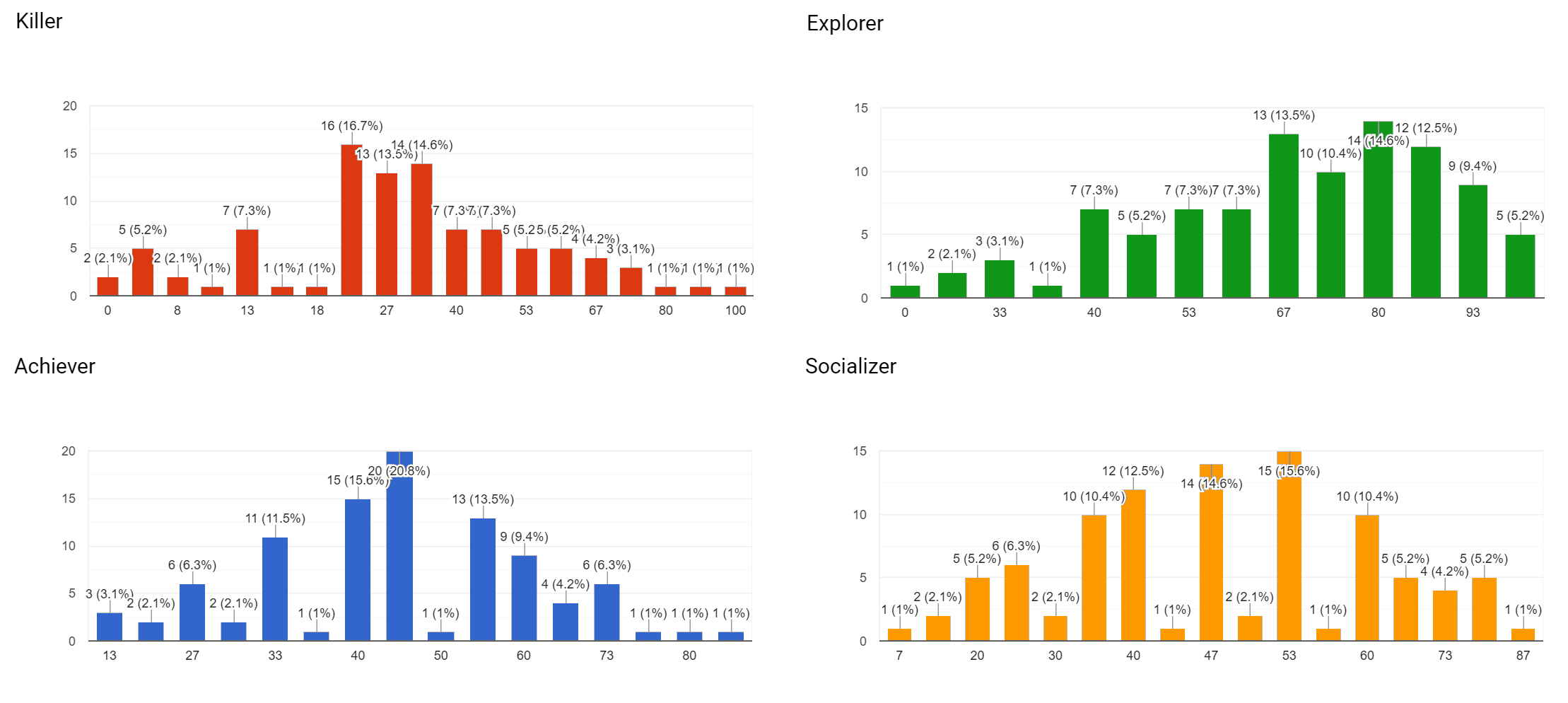
We obtained several fascinating insights from the questionnaire. Although our population sample was very varied in term of how much they played games, we noticed that an overwhelming majority was categorized as Explorer. We theorize that there are 3 possible reasons for this: either our population sample is not uniformly distributed, the underlying distribution of types is not uniformly distributed, or the questionnaire we used to discriminate wasn’t precise enough. Most of the player-base were students and researches, and it could also have been that they are generally more attracted to Explorer traits (that, remember, are more related to understanding the world around).

When we executed the user-study, we had two treatments for the players, to discern if our algorithm was working against. Randomly, for each player and round, we would either turn on or off our personalization algorithm.
This means that sometimes, we adapt the weights to the particular user now playing, whereas sometimes we do not. We had to avoid bias: we needed to discriminate between how general personalization on the population affects the enjoyment, and how much customization at the individual level does. Therefore, we don’t randomly generate weights for when the algorithm is off, but rather take an average of what the population as a whole liked.

This way, we are comparing the adaptation on the individual level against the adaptation to the entire population (what usual play-testing does) instead of against random values.

The table below shows the results:

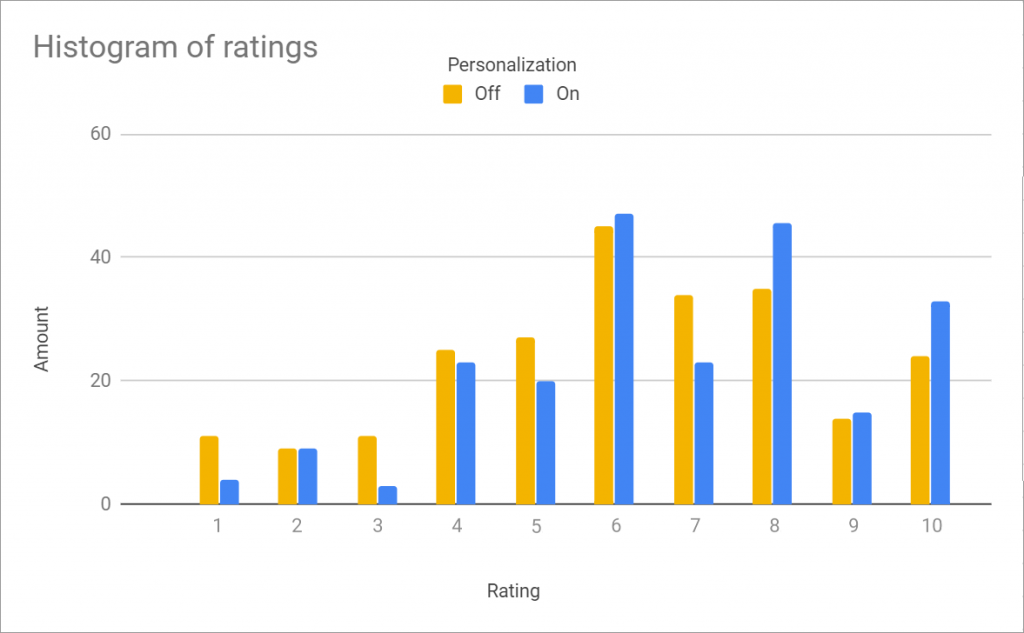
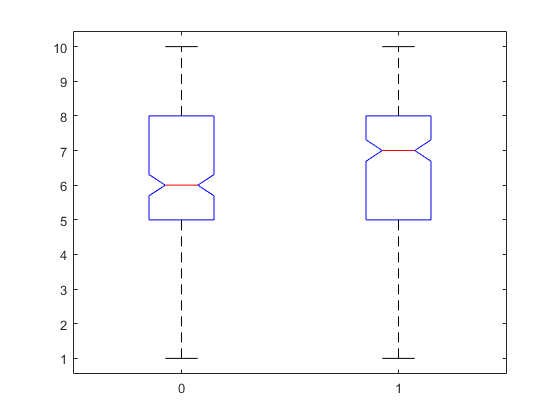
The number of ratings received in each category (1-10 stars). A higher score is better.
ANOVA results. The dotted line represents the range of values in the population, the blue box the 25-75 percentile, the red line the 50 percentile, and the indented segments the range of uncertainty.

We can see that, on average, when our algorithm was turned on, the enjoyment was greater, totaling close to 7/10 stars opposed to around 6/10 when not. Although the difference isn’t as marked as we had hoped, the ANOVA test (Analysis of Variance) further confirmed that the samples come from two underlying populations with high probability. The results aren’t caused by randomness with a high degree of certainty.

This means that our algorithms achieved what it was supposed to. By adapting the level generation to the preferences and playstyle of each user, the enjoyment of the game was increased.

For more discussion of the results, you can check out the thesis here

A correlation matrix of the data collected in the study. Some of the most fascinating results are analyzed in the thesis.

Conclusion

In conclusion, this was a very challenging yet fun project to develop, and I learned a lot along the way. I am happy with the result and, although there were ups and downs, I am pleased with the results we achieved.

I want to take the opportunity to thank once again my supervisors: Prof Dr. Robert W. Sumner, Dr. Fabio Zünd and Henry Raymond for the continued support, and time they dedicated me during the time I spent at the Game Technology Center. I also wanted to thank all the people at the GTC for their time, feedback, and help.

I hope the read was interesting for you if you came this far, and if so, you can check out the game, the thesis and the presentation.

Thanks for reading, cheers! 😄

-Simone

The happy dance performed as ritual upon thesis submission.